힉의 법칙(힉스 로,Hick's Law)이란?

힉의 법칙(Hick's Law)은, 사람이 무언가를 선택하는데 걸리는 시간은 선택하려는 가지수에 따라 결정된다는 법칙이다. 힉-하이먼 법칙(Hick-Hyman Law)이라고 부르기도 한다.

영문 위키피디아 - Hick's Law
한글 위키피디아 - 힉-하이먼 법칙

선택의 가지수가 많아지면 시간이 오래 걸리는 것은 누구나 알고 있었겠지... 그건 너무 당연하니까. 그런 걸 법칙이라고 만든 사람도 다 있나? 실은 내용이 좀 다르다. 대부분의 UI 법칙들을 사람들이 잘못 알고 있듯이, 이 법칙도 대부분의 사람들이 제대로 모르고 있다. 우선 어쩌다가 법칙이 되었는지부터 보자. 

1951년 영국 심리학자 힉은 10개의 램프가 있는 테이블에서 5초 간격으로 임의의 램프가 켜지게 하고 사용자가 그것을 누르는데 걸리는 시간을 측정했다. 이 때, 램프의 개수를 2개에서 10개까지 변화 시키면서 사람들이 선택하는데 걸리는 시간의 변화를 계산했더니, 램프의 개수가 많을수록 시간이 오래 걸렸다. 실험 내용을 보면 어느 정도 유추할 수 있겠지만 사람들이 흔히 잘못 알고 있는 부분을 짚어보겠다.

1. 시간이 확확 늘어나지는 않는다.
우선 이 법칙의 수식을 간단히 살펴보면,

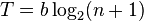
선택지(n)	시간(T)
1	1.0
2	1.6
3	2.0
10	3.5
20	4.3
100	6.6

로 표현된다. 수학에 약한 분들은 오른쪽 그래프를 보면 된다. 처음에는 선택지가 늘어나면 시간이 늘어나는 것 같지만, n이 커지면 시간이 별로 늘어나지 않는다. 어라? 좀 더 정확히 설명하기 위하여 각 경우의 수를 계산해 보면(b=1로 가정), 표와 같이 3개일 때 2초라고 해서, 10개라고 6초 이상 걸리는 것이 아니라 조금 더 늘어날 뿐이고, 20개가 되어도 4.3초 정도 될 뿐이다. 

언듯 생각하기에 선택지가 늘어나면, 시간이 기하급수적으로 늘어나면 좋겠는데... 그래서 UX하는 사람들이 선택을 줄이는 것이 중요하다는 걸 더 강조할 수 있었으면 좋겠는데... 기하급수적으로 늘어나기는 커녕, 선형적으로도 늘어나지 않고... 그냥 로그적으로 늘어난다. 아주 쬐끔씩... 그러니까 이 법칙을 이용하면, "메뉴를 잘게 나누지 말고, 한 번에 많이 보여주어라"는 결론을 주는 것 같다. 어차피 100개에 6.6초지만, 1000개 가운데 고르는데는 9.9초밖에 걸리지 않으니까 말이다. 이상하지 않나?

왜 이런 결과가 나온 걸까?

2. 바이너리 검색에만 해당된다.
기본적으로 여기서 가정하는 것은 (실험에서 느껴졌겠지만) 매우 단순하고 단일한 선택을 인간이 하는데, 10개가 있다면 절반을 나누어 "왼쪽이냐? 오른쪽이냐?" 판단한 후, 오른쪽이라면 다시 5개 가운데, "왼쪽이냐? 오른쪽이냐?"라고 판단하는 식의 논리를 따르는 선택에만 해당이 된다. 그렇기 때문에 1000개나 되더라도, 우선 500개를 제거하고, 다음 250개를 제거하고, 이런 식으로 하기 때문에 많아져도 별로 시간이 늘어나지 않는 것이다. (이런 과정을 Binary Search 혹은 Binary Elimination이라 한다. 수식에서 n+1이 된 것은 하나라도 선택을 할 것이냐 말 것이냐의 선택이 있기 때문이다)

사실 그런데... UI 디자인에서, 이런 식의 선택은 거의 없다. 예를 들어 내가 무엇을 고를지를 알고 있고, 그 대상이 알파벳 순으로 정렬되어 있을 때(!) 적용이 된다. 이런 경우라면, A 보여주고, B 보여주고 이렇게 만들면 정말 짜증이 나고 오래 걸린다. 차라리, A부터 Z까지 한 번에 확 보여주면 더 빠르게 고를 수 있다.

그러나 대부분의 경우는, 화면이 작아서 A부터 Z까지 한 번에 보여줄 수도 없고, 또 그런 식으로 정렬할 수도 없는 아이템인 경우가 대부분이고, 또 그렇게 정렬할 수 있다고 해도, 무얼 선택할지 사용자가 미리 알고 있는 경우도 드물기 때문에 거의 적용이 될 수가 없는 검색 방법이다.

힉의 법칙이 적용되려면,
a. 사용자가 무엇을 선택할지 알고 있고
b. 선택지가 사용자에게 익숙하게 정해진 순서대로 정렬되어 있으며(예를 들면 숫자나 알파벳)
c. 모든 선택지를 한꺼번에 보여줄 수 있을 때(페이징이나 스크롤은 안 됨),

선택지를 그룹으로 나누어 보여주는 것 보다는, 한꺼번에 보여주는 것이 훨씬 빠르다!는 법칙을 적용할 수 있다.

3. 가장 중요한 건 선택의 가지수를 줄이는 방법이다. 
지금까지 본 바와 같이, Hick의 법칙 자체는 사실 써먹을 일이 드문 법칙이다. 따라서, 괜한 아는체 보다는, '상식'에 기대자. 선택의 수가 적으면 선택하는데 걸리는 시간도 짧다. 따라서 선택의 수를 줄이는데 최선을 다 해야한다.

그렇지 않으면 아래 한국어 위키피디아처럼, 이상한 내용을 주장하게 된다. (여기서 이상하다는 말은, 내용이 틀렸다는 것이 아니라 힉의 법칙과 상관이 없거나, 힉의 법칙과 반대된다는 뜻이다)

[필독] 힉스 법칙과 피츠 법칙의 실험, 연구 발전, 그리고 왜 피츠는 인기있는데 힉스는 인기없는가?
[참고] 힉스 법칙과 피츠 법칙을 이용한 선택 시간 계산 및 메뉴 깊이 최적화
[참고] 다중선택에서 결정 시간 최소화를 위한 적응형 최적 과정

[참고##UI법칙##]